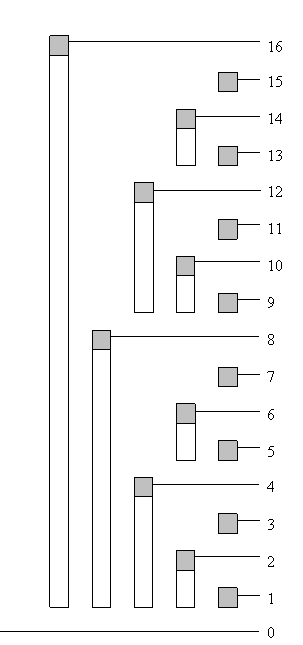我们有时候会遇到这样的问题：
有一个数组arr[0 … n - 1]. 我们需要做下面的事情:

  1. 计算index从 i 到 j 这些数的和。
  2. 修改数组中的某一个数arr[i]

通常有两种做法:

  1. 每次计算从i到j的和的时候，就去从i到j循环累加。这样操作1的时间复杂度为O(n), 操作2的时候复杂度为O(1)
  2. 存储一个前缀和数组sums(prefix sum), 这样计算从i到j的和，就是sums[j] - sums[i - 1]. 时间复杂度为O(1), 但是要修改数组中数的时候，就要修改前缀和数组，时间复杂度为O(n).

两种方法适用的情况不同。我们能不能在O(logn)的时间复杂度下，同时完成修改和求和。有两种算法：

  1. Segment Tree
  2. Binary Indexed Tree

BIT比Segment Tree更好实现，需要的内存也小。
发现解释起来太麻烦，引用里topcoder里的文章也写的很好，这里引用个图吧。

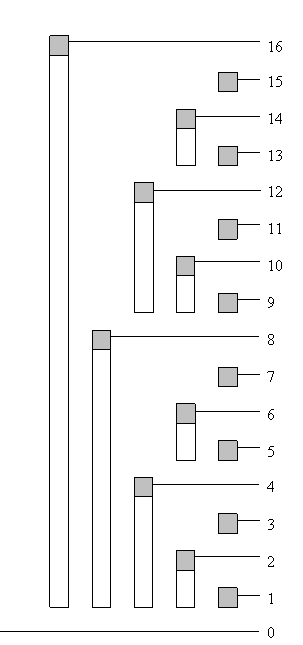
tree of responsibility for indexes

i & (-i) 用来取最后一个1(从左到右)，及其后面的0所组成的数字。
譬如说：20 & (-20). 20 的二进制表示为 10100. 20 & (-20)的结果为4, 二进制为100.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
public class BITree {
    int[] nums;
    int[] BIT;
    int n;
    public BITree(int[] nums) {
        this.nums = nums;
        n = nums.length;
        BIT = new int[n + 1];
        for (int i = 0; i < n; i++) {
            init(i, nums[i]);
        }
    }
    private void init(int i, int val) {
        i++;
        while (i <= n) {
            BIT[i] += val;
            i += (i & -i); //
        }
    }
    public void update(int i, int val) {
        int diff = val - nums[i];
        nums[i] = val;
        init(i, diff);
    }
    private int getSum(int i) {
        int sum = 0;
        i++;
        while (i > 0) {
            sum += BIT[i];
            i -= (i & -i);
        }
        return sum;
    }
    public int sumRange(int i, int j) {
        return getSum(j) - getSum(i - 1);
    }
}

Ref: